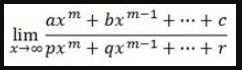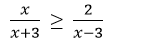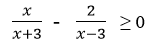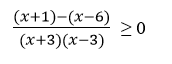Assalamualaikum Wr.Wb…
MAKSIMUM DAN MINIMUM
Andaikan fungsi f dengan domain S,
untuk menentukan nilai maksimum dan minimum, yaitu :
1. Menentukan apakah f
memiliki nilai maksimum atau minimum pada S.
2. Anggap bahwa nilai itu
ada.
3. Menentukan nilai maksimum
dan minimum.
Adapun definisi formal untuk
menentukan nilai maksimum dan minimum adalah sebagai berikut :
Andaikan S, daerah asal f, memuat
titik c, kita katakana bahwa :
(i). f(c) adalah nilai
maksimum f pada S jika f(c) ³ f(x) untuk semua x di S;
(ii). f(c) adalah nilai
minimum f pada S jika f(c) £ f(x) untuk semua x di S;
(iii) f(c) adalah nilai
ekstrim f pada S jika ia adalah nilai maksimum atau nilai minimum.
Akan tetapi, tidak semua fungsi
bisa mencapai nilai maksimum dan nilai minimum, akan tetapi f harus kontinu dan
himpunan S harus berupa selang tertutup sebagaimana teorema berikut :
1. Teorema A :
(Teorema Eksistensi Maks-Min).
Jika f kontinu pada selang tertutup [a, b], maka f mencapai nilai maksimum dan
minimum.
Titik-titik kunci dari teori
maksimum dan minimum terdiri dari tiga jenis titik, yaitu titik ujung, titik
stasioner, dan titik singular. Kemudian yang disebut titik kritis fungsi yaitu
sebarang titik dalam daerah asal fungsi yang termasuk salah satu dari tiga tipe
titik kunci di atas. Seperti yang diterangkan dalam Teorema B berikut :
2. Teorema B
(Teorema Titik Kritis). Andaikan f
didefinisikan pada selang I yang memuat titik c. Jika f(c) adalah titik
ekstrim, maka c haruslah suatu titik kritis; yakni c berupa salah satu :
(i). titik ujung dari I.;
(ii) titik stasioner dari
f(f’(c) = 0);
(iii) titik singular dari
f(f’(c) tidak ada).

Jadi dapat disimpulkan cara
sederhana untuk menghitung nilai maksimum atau minimum suatu fungsi kontinu f
pada selang tertutup I, yaitu :
Langkah 1 Carilah titik-titik
kritis dari f pada I.
Langkah 2 Hitunglah f pada
setiap titik kritis. Yang terbesar adalah nilai maksimum; yang terkecil adalah
nilai minimum.